Key Difference – Insertion Sort vs Selection Sort
Insertion sort and selection sort are two sorting algorithms used to sort a collection of data. Sometimes it is necessary to arrange data in a specific order. Sorting algorithms are mechanisms to sort a set of data. In sorting, the data is arranged according to a numerical or a lexicographical order. If the data is sorted properly, then it would be easy to search data faster. If the phone numbers in a telephone directory are not in a sorted manner, then it would be hard to find a specific telephone number. In the same way, if the words in the dictionary are not arranged in the alphabetical order, it would be very hard to find words. Therefore, sorting is useful in daily life. In Computer Science, there are sorting algorithms to sort a collection of data. Two such algorithms are insertion sort and selection sort. The insertion sort is the sorting algorithm that sorts the array by shifting elements one by one. The selection sort is the sorting algorithm that finds the smallest element in the array and exchanges the element with the first position, then find the second smallest element and exchange it with the element in the second position and continues the process till the entire array is sorted. The key difference between the insertion sort and selection sort is that insertion sort compares two elements at a time while the selection sort selects the minimum element from the whole array and sorts it.
CONTENTS
1. Overview and Key Difference
2. What is Insertion Sort
3. What is Selection Sort
4. Similarities Between Insertion Sort and Selection Sort
5. Side by Side Comparison – Insertion Sort vs Selection Sort in Tabular Form
6. Summary
What is Insertion Sort?
Insertion sort is an in-place comparison-based sorting algorithm. In this method, the array is searched step by step. The unsorted items are moved and inserted into the sorted sublist of the array. The insertion sort algorithm can be explained using the following example.
For example, take the initial array as 77,33, 44,11,88. In this sorting algorithm, the first step is to select the current element.
The current element is 77. The current element is compared with all elements in the left-hand side. The 77, is the first element and there are no elements on the left side. The index of the current position is 0.
Then the index of the current position is incremented by 1. Now the index is 1, and the current element is 33. When comparing it with the element in the left, it is smaller than 77. Then both these values are swapped. Now 33 is in index 0, and 77 is in index1.
Now the array is 33, 77, 44, 11, 88.
Again, the index is incremented. The index is 2, and the current element is 44. It is compared with the elements in the left side. 44 is less than 77. So those two values are swapped. Now the array is 33,44,77,11,88. It is necessary to compare all elements on the left. So, the 44 is compared with 33. 33 is smaller than 44. So those elements do not need to be exchanged.
Now the array is 33,44,77,11,88.
Again, the index is incremented. The index is 3, and the current element is 11. It is compared with all elements in the left. 11 is less than 77, so those two are swapped. Now the array is 33,44,11,77,88. When comparing 11 and 44, 11 is less than 44. So those two are swapped. Now the arrays are 33,11,44,77,88. Again 11 is compared with 33. 11 is less than 33, so those two values are swapped.
Now the array is 11,33,44,77,88.
Incrementing the index will make the index to 4. The value is 88. It is higher than 77. So, there is no need of swapping. Finally, the sorted array is 11,33,44,77,88.
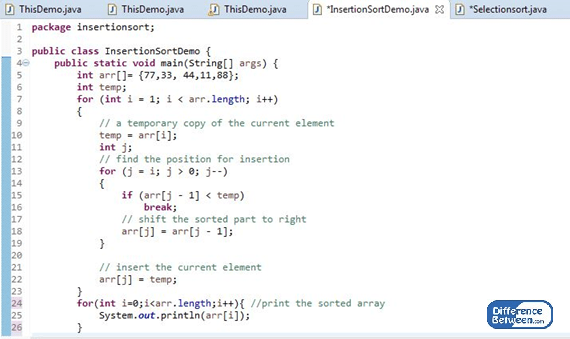
Figure 01: Insertion sort example
The implementation of the insertion sort is as above. The initial array was 77,33, 44,11,88. After sorting, it gives the output 11,33,44,77,88.
What is Selection Sort?
Selection sort is an in-place comparison-based sorting algorithm. The arrays are parted into sections. The sorted part is at the left end. The unsorted part is at the right end. First, the smallest value should be found. Then it is swapped with the left element. Now that element is in the sorted array. This process continues moving unsorted array boundary from one element to the right. The selection sort algorithm can be explained using the following example.
For example, take the initial array as 77,33, 44,11,88,22. In this sorting algorithm, the smallest in the array is found. The smallest element is 11. It is swapped with the element in the 0 index of the array.
Now the array is 11,33,44,77,88,22.
The smallest element is in the index 0, so 11 is now sorted. From the rest of elements, the smallest is 22. It is swapped with the 1st index element.
Now the array is 11,22,44,77,88,33.
The elements 11 and 22 are already sorted. From the rest, the smallest value is 33. It is swapped with the 2nd index element.
Now the array is 11,22,33,77,88,44.
The elements 11,22 and 33 are already sorted. From the rest, the smallest value is 44. It is swapped with the 3rd index element.
Now the array is 11,22,33,44,88,66.
The elements 11,22,33,44 are already sorted. The remaining elements are 88 and 66. The element 66 is swapped with the 4th index element.
Now the array is 11,22,33,44,66,88.
It is the sorted array using selection sort algorithm.
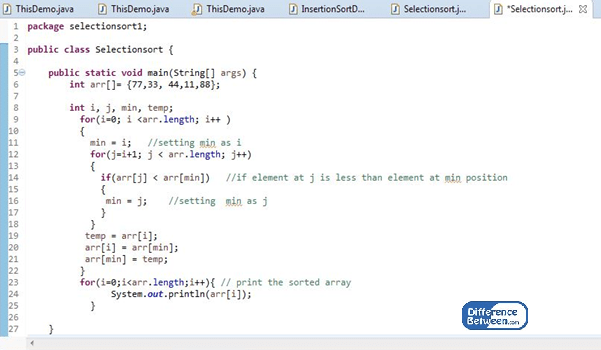
Figure 02: Selection Sort example
The implementation of the insertion sort is as above. The initial array was 77,33, 44,11,88. After sorting, it gives the output 11,33,44,77,88.
What is the Similarity Between Insertion Sort and Selection Sort?
- Both Insertion Sort and Selection Sort are sorting algorithms.
What is the Difference Between Insertion Sort and Selection Sort?
Insertion Sort vs Selection Sort | |
| The insertion sort is the sorting algorithm that sorts the array by shifting elements one by one. | The selection sort is the sorting algorithm that finds the smallest element in the array and exchanges the element with the first position, then find the second smallest element and exchange it with the element in the second position and continues the process till the entire array is sorted. |
| Process | |
| The insertion sort is to sort the sub list by comparing two elements till the whole array is sorted. | The selection sort selects the minimum element and swaps it with the first position, again select the minimum for the rest and swap it will the second position and continue this process until the end. |
| Stability | |
| Insertion sort is a stable sorting algorithm. | Selection sort is not a stable sorting algorithm. |
Summary – Insertion Sort vs Selection Sort
Sometimes it is necessary to sort data. In Computer Science, there are algorithms to sort data. This article discussed the two sorting algorithms which are insertion sort and selection sort. The insertion sort is the sorting algorithm that sorts the array by shifting elements one by one. The selection sort is the sorting algorithm that finds the smallest element in the array and exchanges the element with the first position, then find the second smallest element and exchange it with the element in the second position and continues the process till the entire array is sorted. The difference between the insertion sort and selection sort is that insertion sort compares two elements at a time while the selection sort selects the minimum element from the whole array and sorts it.
Download the PDF of Insertion Sort vs Selection Sort
You can download the PDF version of this article and use it for offline purposes as per citation note. Please download the PDF version here: Difference Between Insertion Sort and Selection Sort
Reference:
1.Point, Tutorials. “Data Structures and Algorithms Insertion Sort.” Www.tutorialspoint.com, Tutorials Point, 8 Jan. 2018.Available here
2.Selection Sorting in Data Structures | Data Structure Tutorial | Studytonight. Available here
3.Theoryapp. “Selection, Insertion and Bubble Sort.” TheoryApp, 20 Jan. 2014. Available here
4.Insertion Sorting in Data Structures | Data Structure Tutorial | Studytonight. Available here
ncG1vNJzZmivp6x7pbXFn5yrnZ6YsqOx07CcnqZemLyue8OinZ%2Bdopq7pLGMm5ytr5Wau261zaycq6yZpLtuv86rq2aZnpl6t7%2BMrJylnZOptrC6jKymq6xf